Orbital Motion

The motion of the planets and stars has been an object of fascination for humans since the dawn of time. With the advent of Newton and Kepler we can what our ancient ancestors could not and actually understand their motion. This page is dedicated to describing the physics behind the simulation you see on thesimulation page. At any point if you get confused try going back to the simulation to see if that helps your understanding.

Circular Motion

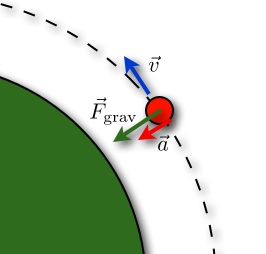
In this context we are employing the mechanics of circular motion to describe the path (location at a given time) and period (time it takes for a body to make a full rotation). It is important to note at this moment that planetary motion is in fact not perfectly circular,generally taking the form of an ellipse, however for the simplified context we can assume the the radius of the orbit(r) is constant throughout any given rotation.

When a body (planet or satellite) is in orbit around a given object it is being effected by 2 general forces. Given Newton's first law:

An object at rest tends to stay at rest, and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an external force.
We can understand this object to moving in a straight line at a constant velocity through space. On the digram this is denoted with the vector (v). However that assumes that there is no acceleration. As the body is not in an isolated system and is joined by another large body (the sun), the object's are attracted to each other. This implies a force between the two. Given newton's law of gravitation:

F = G ^Mm/_r²

• F is the magnitude of the gravitational force between two objects.
• G is the gravitational constant (6.67*10¹¹m³kg^-1s^-2)
• M and m are the masses of the two objects.
• r is the distance between the centers of mass of the two objects.

We can see than there is a force that accelerates the objects towards each other. However as the body still moves in accordance with Newton's first law the vectors (two forces) combine to create a circular motion. This is called the centripetal force or the force that acts towards the center of the circular orbit, continuously changing the direction of the planet's velocity and keeping it in orbit. To investigate the consequences of this I encourage you to return to thesimulation page and play around with the values for orbiting mass and orbing radius. For more clarity you can see this phenomon being representing in the force diagram below.

Period

Now that we know why planets orbit the next natural question is to investigate it's speed. We all know that the sun revolves around the earth once roughly every 365 days or every year, but why is that? This depends on three values, the mass of the orbiting object (m), the mass of the body it is orbiting (M or the sun) and the distance between the two (r). So given two masses are orbiting eachother (M = sun, m = other object) we can understand there force to follow newton's law of gravitation. Using Newton's third law:

F=ma or F = ^mv2/_r
We can rewrite the entire equation as this:

G ^Mm/_r² = ^mv2/_r
Here something quite beautiful happens where the small (m)s or mass of orbiting object cancel out and simplifying it we are left with:

^GM/_r² = v ²
v = √^GM_r
Thinking about it for a little bit we can understand that the time it takes for an object to go around in a full rotation is the circumference divided by the velocity (m divided by meters per second). Rearranging the equation for T period:

T = ^2πr/_√^GMr
Further simplifications makes

2π * √^r3/_GM
Now we can plug in numbers to this equation, feel free to test it out on the simulation page

Gravitational Potential Energy

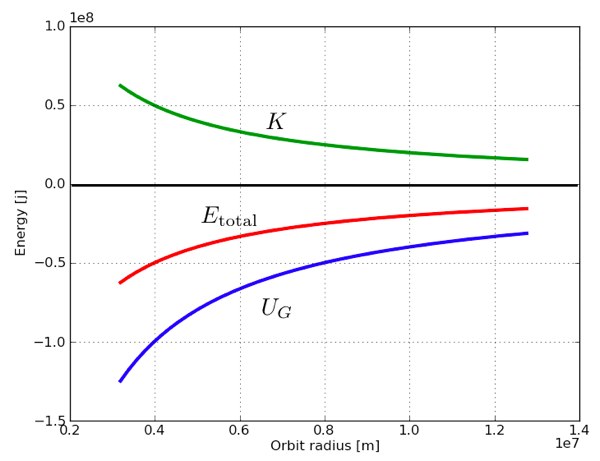
Energy in orbit is still comprised of the same things Kinetic Energy (KE) and Potential Energy (PE). More specificly the total energy is the sum of KE and PE. Kinetic energy is still

Around a point-like object, the gravitational potential is singular as the distance decreases to zero, thus you can't use it as a ground potential. The only meaningful alternative to use the infinite distance as zero potential. But, to preserve energy, objects coming from near-infinite, they get kinetical energy, this is coming by the decrease in the gravitation well. Thus the gravitational energy should be negative. If you revert the convention, i.e. to have a positive gravitational potential, then you should revert also the kinetical energy. It is weird or you have to find a different zero reference point (it also weird + occasional, you have to explain, why) or you will harm energy preservation (-> give up useful physics) Note, if you calculate some easy thing, for example you are calculating the gravitational energy of an elevator in a high school homework task, you can use the ground as zero reference without any problem. It falls to (2): you essentially selected 6636km distance as zero potential in the gravity well of the Earth. KE = ^1/₂mv² Which we can throw in our previously calculated formula of velocity to calculate as:

Potential Energy